Late in 2017 Ironman announced a new system for Kona 2019 Pro Qualifying, moving to a slot-based system almost equal to the agegroup qualifying system. One aspect of the system is “unassigned slots” for some races that will be “assigned according to the ratio of starting Pro Athletes” (as stated in the official “Ironman World Championship Profession Athlete Qualification“). The specific details of the assignment algorithm is considered private by Ironman. Based on the first races and the resulting slot assignments Russell Cox (who is focused on the agegroup side, his data can be found at http://coachcox.co.uk) and I have done our best to reverse engineer this algorithm. This post looks at the available data, potential algorithms and the conclusions that can be drawn. This “algorithm post” will be followed in the next days by one looking at alternative approaches and an “opinion post”.
Data on Races With Unassigned Pro Slots
Here’s a quick look at the Pro races with unassigned slots so far:
- IM Arizona – 2 MPRO slots (based on 15 female and 32 male Pros starting the race) plus 1m+1f base slot
- IM Western Australia – 1 Pro slot each (based on 10 female and 13 male Pro starters) plus 1m+1f base slot
- IM Mar del Plata (South American Regional Championship) – 2 MPRO slots (based on 15 female and 23 male Pro starters) plus 2m+2f base slots
In addition, Ironman has stated that they use the same algorithm for determining the slot assignment for the agegroups, so we can also cross-reference if the “suspected” algorithm also fits the agegroup slots.
Assignment Algorithms
There are a number of algorithms dealing with a similar problem to slot assignment. Typically, they come from a voting context, where a small number of indivisible “seats” (usually tens to hundreds) has to be assigned based on “votes” (usually thousands). Even though the US voting system is typically majority-based, it also has to deal with a number of “representational” issues. One example is assigning a fair number of seats in the House of Representatives (capped at 435 seats) to the States in relation to their population (total US population based on the 2010 census 308.7 million, with state populations between 37.25 Million and 0.56 Million).
This post looks in detail at the two most widely used approaches, the Hamilton and Jefferson methods using the size of the field as the basis for the slot assignment. Different approaches such as depth of field will be discussed in a follow-up post. When working off the size of the field, it seems best to apply the algorithm to the number of athletes starting the race. The number of registered athletes is often quite different from the number of athletes actually racing, especially on the Pro side. And the number of finishers isn’t finalized for some time during and after the race (especially considering DQs that might be contested for days or weeks), and DNFs often contain an element of bad mechanical luck.
Hamilton Method
The Hamilton Method, also know as Hare-Niemeyer or “Largest Remainder”, is one of the oldest systems of assigning seats. It calculates the number of votes required for a seat by dividing the total number of votes by the number of seats available and then divides the votes a party has received by this number. Another way to put this is that it multiplies the number of available seats with the fraction of votes a party has received. This calculation results in a number with an integer part and a fractional part. According to Wikipedia:
Each party is first allocated a number of seats equal to their integer. This will generally leave some seats unallocated: the parties are then ranked on the basis of the fractional remainders, and the parties with the largest remainders are each allocated one additional seat until all the seats have been allocated.
In the context of Kona slots, the Hamilton Method multiplies the number of slots with the number of starters in a group divided by the total number of starters. The algorithm is probably easier to understand with a few examples.
Hamilton Method on Unassigned Slots
The first suggested algorithm applies the Hamilton method to the number of unassigned slots. (Russ and I believe that this is the “old” method of assigning agegroup slots that was used until the summer of 2018.)
For the Pros, there are two unassigned slots. Using IM Arizona as an example, we get the following calculations:
| Arizona | Starters | Quota |
| Men | 32 | 1.36 (2* 32/47) |
| Women | 15 | 0.64 (2* 15/47) |
| Total | 47 | 2 slots |
This means that the men get one slot (the integer part of their ratio), while the second slot would go to the females (as their fractional part of 0.64 is larger than 0.36). As both unassigned slots at IM Arizona went to the men, this is obviously not the algorithm that is used for the 2019 qualifying season.
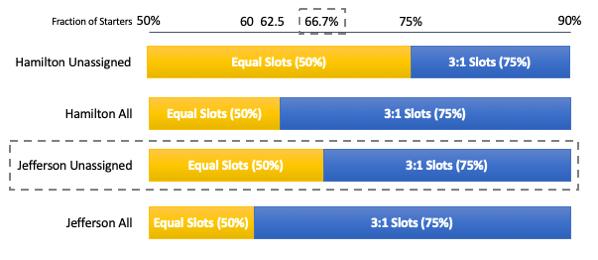
If you look at this type of calculation, then the larger agegroup will have to be at least three times as large as the smaller one to get both slots (i.e. 75% of the whole Pro field):

Obviously this is a very tough requirement, and therefore not very useful to achieve “proportional slots” for the Pros when assigning only two slots. It’s also not fair that the men will always have a smaller fraction of slots than their fraction of the Pro field. It’s a bit of speculation, but I think that Ironman also felt that the system they have been using so far for assigning agegroup slots doesn’t work well for the small number of Pro slots, and that’s why they decided to change their algorithm going into the Kona 2019 qualifying season.
Hamilton Method on All Slots
Another approach would be to apply the Hamilton method on all slots while observing “minimum” slots. Again using Arizona as an example:
| Arizona | Starters | Quota |
| Men | 32 | 2.72 (4* 32/47) |
| Women | 15 | 1.28 (4* 15/47) |
| Total | 47 | 4 slots |
This would result in the men getting three slots: two from the integer part of their ratio, and another one because 0.72 is larger than 0.28) – the minimums are already observed in this example. In order for the larger agegroup to get three slots, they would need more than 5/3 of the smaller agegroup or at least 62.5% of the field:

While this method gives the observed slot assignment in Arizona, IM has stated that their assignment process is based on the number of unassigned slots and not all slots. It’s also tricky to extend this algorithm to include minimum slots for the bigger number of agegoups for all cases. (For the technically minded: The minimum slots plus the integer parts may already assign more slots than available.) It’s very unlikely that this is the method used by Ironman.
Jefferson Method
The Jefferson Method (also known as D’Hondt method) uses a larger number of operations to determine the slots:
The total votes cast for each party is divided, first by 1, then by 2, then 3, up to s, the total number of seats. The winning entries are the s highest numbers in the whole grid; each party is given as many seats as there are winning entries in its row.
Similar to the Hamilton Method, it can be applied to all slots or only those that are unassigned.
Jefferson Method on Unassigned Slots
Based on the unassigned slots, here’s the resulting Jefferson grid for IM Arizona:
| Arizona | Starters | 1 | 2 |
| Male | 32 | 32 | 16 |
| Female | 15 | 15 | 7.5 |
| Total | 47 | 2 slots | |
There are two unassigned slots, and as the male starters divided by 2 is larger than the number of females starters, both “winning entries” are from the men and both slots would get assigned to the MPROs. This fits the slot assignment in Arizona.
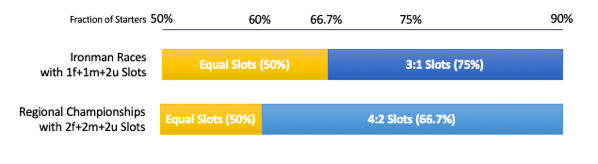
In general, to get both unassigned slots the larger agegroup needs to have at least twice as many starters as the smaller one, i.e. at least two thirds or 66.7% of the whole Pro field:

Jefferson Method on All Slots
As for the Hamilton Method, we can also apply Jefferson Method for all available slots while observing minimums.
| Arizona | Starters | 1 | 2 | 3 |
| Male | 32 | Auto | 16 | 10.34 |
| Female | 15 | Auto | 7.5 | 5 |
| Total | 47 | 4 slots | ||
Observing minimums is relatively straightforward in the Jefferson Method – instead of starting with the divisor 1, you start with the first divisor that is larger than the minimum. As there is one minimum slot for each, the Divisors start with 2, and again the two unassigned slots would go to the men. For Arizona, this approach would also yield the “observed” 3:1 slots, but as we know that two more WPRO starters would have changed the slots, this can’t be the actual algorithm.
In order to get both slots using this approach, the larger agegroup needs to have at least 60% of the starters:

Conclusion .. For Now
Here’s an overview of the different approaches so far:
Based on the text in the Pro Qualifying Rules (referencing “the ratio of starters to Unassigned Slots”) and the fact that the correct Arizona distribution is yielded by the Jefferson Method on Unassigned slots, I thought that I had identified the method used – that’s why it’s highlighted in the graph shown above. Russ provided further evidence from the age-group side that was supposedly using the same algorithm. (More on the agegroup side of things in Russell’s post on Age Group Kona Slot Allocation.) It also correctly predicts an even split of Pro slots for IM Western Australia. But we have not reached the end of the story yet …
Slot Assignment For Regional Championships
Regional Championships have a different number of slots: While they also have two unassigned slots, they offer two base slots each for the men and women. (IM Arizona has one slot each, plus two unassigned slots.) But as the Pro Qualifying Rules state that the slots are assigned based on “the ratio of starters to Unassigned Slots”), I was confident that there would be even slots in Mar del Plata. Here’s Jefferson Grid for Mar del Plata:
| Mar del Plata | Starters | 1 | 2 |
| Male | 23 | 23 | 11.5 |
| Female | 15 | 15 | 7.5 |
| Total | 38 | 2 slots | |
However, the actual slot assignment was that both slots went to the men, resulting in the final numbers of four slots for the men and two for the women. So we need another twist to the algorithm.
It seems reasonable that the distribution for the unassigned slots is slightly different when there are two base slots as the resulting “uneven distribution” is 3:1 (or 75%) in case of the normal races and 4:2 (or 66.7%) for the Regional Championships. If the Jefferson Method on Unassigned Slots were used, then the fraction of slots for the larger agegroup would always be lower their fraction of starters.
Jefferson Method On All Minus 2 Slots
As the Jefferson Method has been working remarkably well for the Ironman races with just one base slot each, I was looking for slight tweaks to get the right results for Mar del Plata and some of the variations. (Apparently, one more WPRO or one less MPRO would have changed things for Mar del Plata.) This “tweaking” results in the “Jefferson All Minus 2” method:
| Mar del Plata | Starters | 1 | 2 | 3 |
| Male | 23 | Auto | 11.5 | 7.67 |
| Female | 15 | Auto | 7.5 | 5 |
| Total | 38 | 4 slots (1 each minimum) | ||
This method is equivalent to the Jefferson Method on Unassigned Slots except for the Regional Championships that offer two base slots each. (In addition, it’s the same for agegroups as there is always a minimum of one slot there.)
For the Regional Championships, there is a minimum of 60% of the field needed in order to get both unassigned slots:

Conclusion
Going forward, the “Jefferson Method on All Minus 2 Slots” will be the algorithm I’ll be using to predict how the slot assignments will look like. New results will either send me back to the drawing board, but hopefully they will strengthen the evidence that this is indeed the algorithm Ironman currently uses.
Based on this algorithm, the “inflection points” for the slot assignments are 66.7% of the Pro starters for “regular” Ironman races with unassigned slots and 60% for the Regional Championships: